1.
i
На координатной прямой отмечены точки O, A, B, C, D, F.
Если координата точки A равна 
то числу 1 на координатной прямой соответствует точка:
1) C
2) B
3) D
4) F
5) O
РЕШУ ЦТ — математика
Вариант № 34499
Поэтому необходимо отсчитать от нуля 7 делений — это точка B.2.
i
Пусть O и O1 — центры оснований цилиндра, изображенного на рисунке. Тогда образующей цилиндра является отрезок:
1) AB
2) AC
3) AD
4) AO
5) OO1
3.
i
Арифметическая прогрессия (an) задана формулой n-го члена an = 6n + 1. Найдите разность этой прогрессии.
1) 7
2) 5
3) −5
4) −6
5) 6
где d — разность арифметической прогрессии. Коэффициент перед n и есть разность арифметической прогрессии, он равен 6.4.
i
Если 16% некоторого числа равны 28, то 60% этого числа равны:
1) 119
2) 112
3) 91
4) 98
5) 105
где x — неизвестное число.
5.
i
Укажите номер выражения, являющегося одночленом восьмой степени:
а) 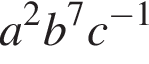 | б) 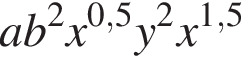 | в)  | г) 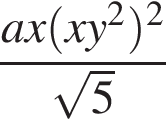 | д)  |
1) а
2) 6
3) в
4) г
5) д
6.
i
Величины a и b являются прямо пропорциональными. Используя данные таблицы, найдите неизвестное значение величины a.
| a | 2,9 | |
| b | 114 | 8,7 |
1) 43
2) 33
3) 39
4) 13
5) 38
7.
i
Длины катетов прямоугольного треугольника являются корнями уравнения x2 − 9x + 10 = 0. Найдите площадь треугольника.
1) 10
2) 9,5
3) 9
4) 5
5) 4,5
8.
i
От листа жести, имеющего форму квадрата, отрезали прямоугольную полосу шириной 2 дм, после чего площадь оставшейся части листа оказалась равной 15 дм2. Длина стороны квадратного листа (в дециметрах) была равна:
1) 5
2) 6
3) 7
4) 8
5) 9
Тогда:
9.
i
Дан треугольник ABC, в котором AC = 21. Используя данные рисунка, найдите длину стороны AB треугольника ABC.
1) 10,5
2) 9,6
3) 11,8
4) 10,2
5) 9,4
10.
i
Из точки A к окружности проведены касательные AB и AC и секущая AM, проходящая через центр окружности O. Точки B, С, M лежат на окружности (см. рис.). Известно, что BK = 4, AC = 9. Найдите длину отрезка AK.
1) 
2) 
3) 
4) 
5) 
11.
i
Укажите уравнение, равносильное уравнению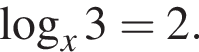 
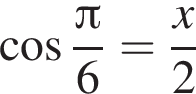
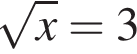
1) 
2) 
3) 
4) 
5) 
уравнение 4 имеет корень 
уравнение 5 имеет корень 
Решим третье уравнение:
12.
i
Свежие фрукты при сушке теряют a % своей массы. Укажите выражение, определяющее массу сухих фруктов (в килограммах), полученных из 35 кг свежих.
1) 
2) 
3) 
4) 
5) 
13.
i
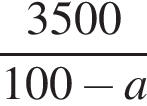
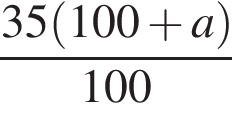
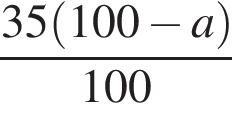
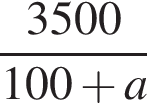
Уравнение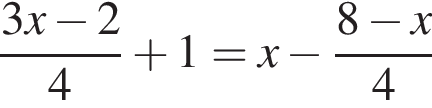 
равносильно уравнению:
1) 
2) 
3) 
4) 
5) 
14.
i
Упростите выражение
1) 
2) 
3) 
4)
5) 
15.
i
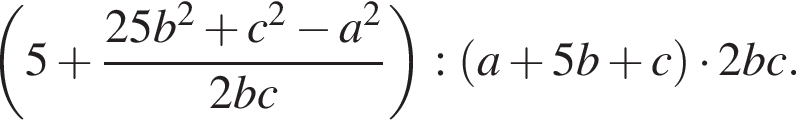
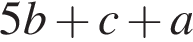
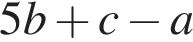
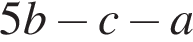
Строительная бригада планирует заказать фундаментные блоки у одного из трех поставщиков. Стоимость блоков и их доставки указана в таблице. При покупке какого количества блоков самыми выгодными будут условия второго поставщика?
| Поставщик | Стоимость фундаментных блоков | Стоимость доставки фундаментных блоков |
|---|---|---|
| 1 | 240 | 1900 |
| 2 | 255 | 1020 |
| 3 | 300 | бесплатно |
1) более 22
2) от 15 до 45
3) от 23 до 58
4) менее 59
5) от 22 до 59
16.
i
ABCDA1B1C1D1 — прямоугольный параллелепипед такой, что
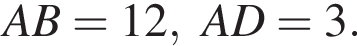Через середины ребер AA1 и BB1 проведена плоскость (см.рис.), составляющая угол 60° с плоскостью основания ABCD. Найдите площадь сечения параллелепипеда этой плоскостью.
1) 
2) 
3) 
4) 
5) 
таким образом:
17.
i
Найдите сумму корней уравнения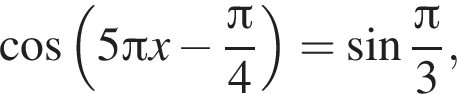 
принадлежащих промежутку [–1; 1].
1) 0
2) 0,1
3) 0,4
4) 0,5
5) 2,1
18.
i
Корень уравнения
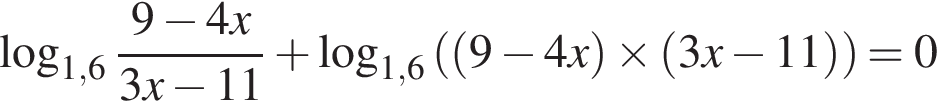
(или сумма корней, если их несколько) принадлежит промежутку:
1) 
2) 
3) 
4) 
5) 
19.
i
Для покраски стен общей площадью 125 м2 планируется закупка краски. Объем и стоимость банок с краской приведены в таблице.
| Объем банки (в литрах) | Стоимость банки с краской (в рублях) |
|---|---|
| 2,5 | 85 000 |
| 10 | 260 000 |
Какую минимальную сумму (в рублях) потратят на покупку необходимого количества краски, если ее расход составляет 0,28 л/м2?
л краски. Можно купить 3 банки по 10 литров и 2 банки по 2,5 литра, тогда сумма составит 
20.
i
Найдите сумму корней (корень, если он единственный) уравнения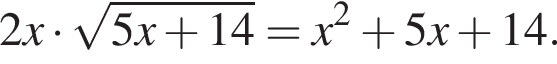 
Тогда:
21.
i
В равнобедренную трапецию, площадь которой равна 
вписана окружность. Сумма двух углов трапеции равна 60°. Найдите периметр трапеции.
Сумма углов в равнобедренной трапеции, прилежащих к одной стороне равна 180°, откуда следует, что сумма углов, данная в условии — есть сумма углов при основании AD, которые равны. 
Поэтому из площади трапеции найдем x:
22.
i
Пусть (x1; y1), (x2; y2) — решения системы уравнений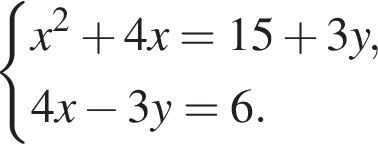 
Найдите значение выражения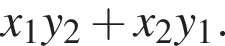 
23.
i
Найдите значение выражения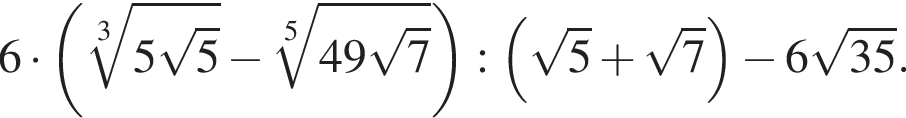 
24.
i
Если x0 — корень уравнения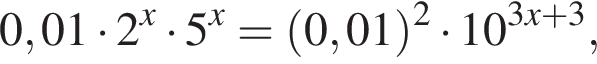 
то значение выражения 
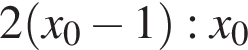равно... .
25.
i
Решите уравнение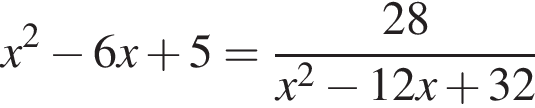 
и найдите сумму его корней.
Получим:
найдем по теореме Виета, она равна 9.
равносильно уравнению 
искать ОДЗ не требуется.26.
i
Найдите значение выражения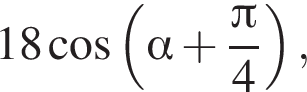 
если 
27.
i
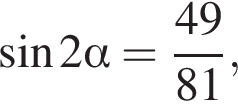
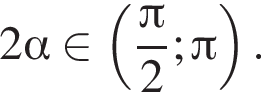
Найдите сумму целых решений неравенства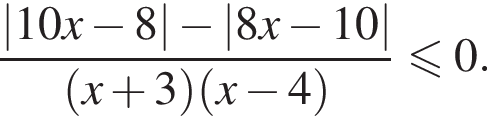 
совпадает со знаком разности 
имеем:
корни знаменателя 
Поэтому: 
Целые решения — числа −2, -1, 1, 2, 3. Их сумма равна 3.28.
i
Из точки А проведены к окружности радиусом 
касательная AB (B — точка касания) и секущая, проходящая через центр окружности и пересекающая ее в точках D и C (AD < AC). Найдите площадь S треугольника ABC, если длина отрезка AC в 3 раза больше длины отрезка касательной. В ответ запишите значение выражения 2S.
Обозначим AB за x, тогда 
Тогда: 
при этом 
Получим: 
Тогда площадь треугольника ABC: 
29.
i
Пусть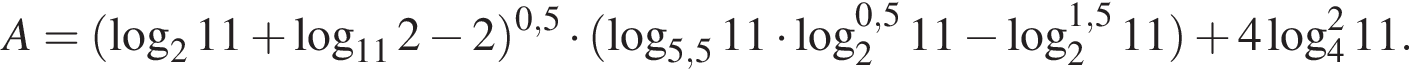 
Найдите значение выражения 2A.
Тогда имеем:
30.
i
Трое рабочих (не все одинаковой квалификации) выполнили некоторую работу, работая поочередно. Сначала первый из них проработал 
часть времени, необходимого двум другим для выполнения всей работы. Затем второй проработал часть времени, необходимого двум другим для выполнения всей работы. И, наконец, третий проработал часть времени, необходимого двум другим для выполнения всей работы. Во сколько раз быстрее работа была бы выполнена, если бы трое рабочих работали одновременно? В ответ запишите найденное число, умноженное на 12.
времени на выполнение всей работы, в то время, как первый за 
работы. 
времени на выполнение всей работы, в то время, как второй за 
работы. 
времени на выполнение всей работы, в то время, как третий за 
работы. 
то они выполнили бы работу за: 
Поэтому, работая вместе работа была бы выполнена в 
раза быстрее. В ответе будет число 